“I participated in an Influencer Activation on behalf of Influence Central for MedImmune. I received product samples to facilitate my review as well as a promotional item to thank me for my participation.”
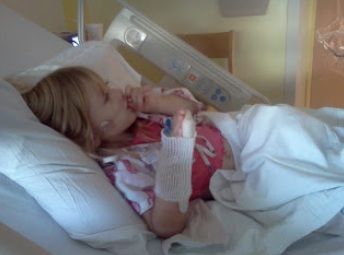
I had never heard of RSV until 3 years ago when my daughter who was two years old at the time contracted it and was hospitalized. She started wheezing so I took her to the doctors. At the doctors they gave her nebulizer treatments that didn’t seem to help her so they sent us for chest x-rays and from that short distance from the doctors to from the x-rays she because completely lethargic. I was scared. This is my baby, what was happened to her? Then I was sent back the doctors office where they admitted her to the hospital.
Once admitted and tests were run the results showed she had RSV, pneumonia, asthma and a partial collapsed lung accompanied with a bacterial infection! For several days she remained in the hospital on oxygen, treatments and antibiotics. And after her lung healed and the RSV cleared up she was released from the hospital and she was back to her feisty self. As a mom seeing my daughter in the condition was heartbreaking! Since then has has been sick several times not with RSV but asthma related illnesses.
World Prematurity Day is November 17th. Although I do not have any preemie babies of my own I do know other moms who do. I couldn’t imagine what a family goes through when a baby is born very early and may encounter several obstacles along the way. I am very thankful that my 5 children were born full term and pray that if we are blessed with a 6th baby that that baby too be born a healthy full term baby.
So what exactly is RSV? It is a common seasonal virus which is contracted by children by the age of two and typically causes mild to moderate cold-like symptoms in healthy, full-term babies. Epidemics occur typically from November through March, though it can vary by geography and year-‐to-‐year.
RSV can be detected by a few quick ways:
~ Persistent coughing or wheezing
~ Bluish color around the mouth or fingernails.
~ Rapid, difficult, or gasping breaths
~ Fever over 100.4°F (rectal) in infants under 3 months.
In the case of my daughter she had most of these signs and I did not even realize what was going on. I was so scared she was going to die because it hit her hard and fast. She was completely out of it.
My greatest blessings are these 5 precious little ones, I never want to experience what my husband and I went though with our daughter again!
For more information about RSV and ways to prevent it by visiting RSV.com. Talk to your doctor about RSV, and watch for signs and symptoms. You can sign up to receive some fact sheets and/or questions to ask your Dr at RSVProtection.com.
“I participated in an Influencer Activation on behalf of Influence Central for MedImmune. I received product samples to facilitate my review as well as a promotional item to thank me for my participation.”
Mama to 5 Blessings is disclosing this in accordance with the Federal Trade Commissions 16 CFR, Part 255 Guides Concerning the Use of Endorsements and Testimonials in Advertising.


















RSV is such a scary thing. My boys never had RSV thankfully and I hate to think about any baby being so sick 🙁
RSV scares the heck out of me. I hate that our little ones who are the most defenseless are prone to it.
I know, right? Of all people, it effects the most innocent.
I’ve never heard of RSV before so thank you for making me aware. Sounds like such an awful and scary thing to go through. I hate hearing of little ones being so sick 🙁
Aww. I’m so sorry to hear your daughter was so sick. Thanks for sharing this post. RSV is one of those things that can really hurt a child, but a lot of people don’t know about it.
RSV is a horrible thing for a family to go through. I do have one friend that experienced it and learned all about RSV then.
Wow, i have just recently started to hear about this… It is very bad. I am glad my kids did not have this.
I know a little bit about RSV – enough to know that it’s a really scary illness for babies! One of my friends just told me last week that her son had RSV!
RSV is more serious than I initially though. Thanks for the thorough information, sharing with my expecting friend!
This is such a scary illness. One of my kids was tested for this but luckily it wasnlt the illness.
This is such a scary illness. One of my kids was tested for this but luckily it was not RSV.
When my pediatrician told me about this, I was totally freaked. Thankfully, my son never got this. It’s a scary thing.
Nope, had never heard of RSV until now. I probably would have though it was just a common cold or flu!
My daughter had RSV when she was little. We caught it early on so she did not have to be hospitalized. So glad to see your daughter is okay!
Thank you for the great information. I will share it with my friends that have little ones. I am glad you daughter is feeling better.
OMG!! That is so scary! I wonder if that is what my DS had when he was 6 months old. IT was so scary!! He didn’t get to the point of hospitalization but was on a nebulizer for months!
Great post, your kids are adorable. Definitely sharing this post with my friends.
What a horrible illness! I’m so blessed that my daughter never came down with it. I’m sorry your little one had to endure it!
This year was the first time I heard about it when my friends daughter had it. I’m so glad they are bringing awareness to such a scary illness.
That must have been such an awful thing to go through. My daughter has asthma and I know it’s not fun when she’s in the ER.
RSV prevention is so important. Thanks for sharing this information with all of us.
Never really heard of it!! Glad I know now 🙂
Wow. thank you so much for informing me.. Will definitely check now!
RSV is so scary. One of my nephews had it and had to be hospitalized for a little while.
How scary to have such a sick little girl! Glad she’s okay now! RSV is so scary! We will be using extra precautions in this RSV season!
I’ve been a premature baby and was born after 7 months. I had to stay at an incubator for 45 days. I did turn out ok growing up. I hope your daughter gets a lot healthier.
I’ve actually never heard of RSV, so thanks for writing about it! I’ll definitely be more aware of it now!
Thanks for sharing this information! I had heard of RSV but didn’t know what it was. It must have been really scary to have a baby that sick.
I never knew about RSV. It looks so scary. Thank you for educating us on it.
Thanks for this post. I didn’t know anything about RSV until I read this. What a scary sickness!
I have never heard of this before. Thank you for sharing this with everyone. I love the photo of your kids. They’re very adorable!
RSV is very scary, and very serious. I remember being shocked when I did a project on it in college.
Thank you so much for sharing about this. I believe RSV was missed for so long in my older daughter and now she has residual issues with her lungs. 🙁 Thankfully, they caught it early in my other daughter.
When my nephew was a baby, we had an RSV scare. It turned out to be something else, but it scared the crap out of all of us.
I thought RSV so only in infints? Im so sorry you had to go through this.
Awwies. I am soo sorry your baby had to go through this. I have heard of RSV and it’s not a pretty thing at all. Thank God she is alright!
Thank you for sharing your story. I can not imagine how scary that must have been for you. By sharing your story you are helping others. Thank you.
I know a family recently affected and it is so scary. Thank you so much for sharing this info!
RSV is so scary. My little girl had it to, although not as severe. I am so grateful for modern medicine!
I can only imagine how scary that was for you and your family. I know how worried I get when anything happens to my daughter. I hope she is feeling back to normal!
I know several mom’s with new preemie babies this year. This is such great information to pass along.
Thanks for sharing this information. Awareness will help many mothers.
Never heard of RSV but it can be a mother’s nightmare.
I’m so sorry you had to go through that! Thank you for sharing this info!
My daughter tried coming out two months early. I was put in bed rest for my last two months of pregnancy. I was so afraid to have a preemie. Great information.
I was very lucky and my kids did not get RSV. When they were born i was not even told about it.
Wow, RSV is serious. Thank you for bringing awareness to it.
How heartbreaking! I know I would’ve been scared to death! So happy she is ok and thank you for the info I’m going to forward it onto my mommy friends
RSV is so scary! I am so thankful that none of my precious babies suffered from it. Thank God!
RSV is very scary, I’m glad none of the babies in my family ever got it.
RSV is extremely scary, I am very lucky having given birth to a preemie we were not affected. Thanks for the great info
RSV is terrible. It is very scary for the parents and hard on our little ones. Great article.
Insightful read! Will pass along to a friend of mine!
I’m a huge fan of protecting our kiddos. This is such a scary and contagious virus. Thanks for all the info.
Very Scary. My nephew ended up in the hospital with this last year.
Wow, this is so scary but I am so glad she made a complete recovery. I am glad you informed us of this.